本文启发自知乎问题:极坐标表示 5000 到 50000 之间的素数画点到纸上为什么会形成一条斐波那契螺旋线?
把一个自然数n用极坐标表示,也就是在坐标(n*cos n,n*sin n)的位置绘制一个点;而当你把所有素数绘制到纸上之后,会发现它是一个包含了许多条空白线条的圆形:
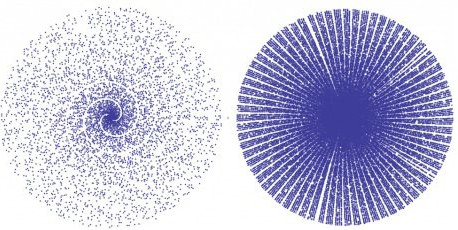
很显然,空白是合数导致的,但为什么合数会排列成一条条曲线呢?
王小龙已经做了精彩的回答。不过为了更直观地理解,我写了这个小程序:
用法超简单:可以任意拖动、点击右下角的“+”、“-”来缩放显示范围,“#”重置。
当数字范围较小时,能看到明显的两条白色螺旋曲线;而数字范围变大到一定程度后,会变成接近直线的71条白线,但向外拖拽后,会发现这些直线也逐渐有了弧度。
由于图形是实时生成的,考虑到电脑性能问题,所以对数字范围做了限制,如果需要更深入研究,请使用专业数学软件。
jtj5ujn75i7i