在n个外观完全相同的小球中,有一个与其它球重量不同。如何只用一架天平找到这个球并判断它比其它球轻还是重?最少需要称几次?
这是一个流传极广的经典问题,在网上随便一搜就会发现无数人都提出了自己的见解和算法并争论不休。最常见的是12个小球,至于更多球的计算,就不是人力能及的了。
实际上,这个问题确实是有准确答案的:n次称量最多可以在![]() 个球中找到不同的球,并判断它的轻重。
个球中找到不同的球,并判断它的轻重。
理论证明可参考The Problem of the Pennies, F. J. Dyson, The Mathematical Gazette , Vol. 30, No. 291 (Oct., 1946), pp. 231-234。
不过这里不打算讲那么多理论,而是直接演示怎么称量并找到这个小球。
算法十分精巧,我尽可能简单地描述了一下。如果还是觉得太抽象,没关系,直接点击这里或者拉到下面看演示就可以了。
- 编码:
知道了球数,就能算出需要称量几次;
以这个次数作为长度,使用0、1、2排列组合进行编码,如001021、212022等等,再去掉全0、全1和全2,可知一共有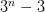 个编码;
个编码;
如果在一个编码中,第一处相邻数字不同的情况是01、12或20,则我们称它为正序码,如1120021;
否则为逆序码,如2221012;
在长度为n的编码中,正序码和逆序码的数量相等,均为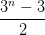 个。
个。 - 赋值:
如果把一个正序码中的0换成1,1换成2,2换成0,则它仍然是正序码;
根据这个原理,我们把所有正序码按3个3个进行分组,如12001、20112、01220这3个就是一组;
把正序码一组一组地分配给小球,每球一个,直到分完;
然后把每个正序码的0换成2,2换成0,它就变成了一个逆序码,如12001变成10221;
这样,每个小球就有了两个编码,一个正序,一个逆序,而且所有球都不重复。 - 称重:
第一轮,我们把所有正序码第一位为0的小球放在天平左侧,为2的小球放在右侧,其它的放在旁边;
如果天平左倾,记为0;右倾,记为2;平衡,记为1;
然后是第二轮,把第二位为0的小球放在左侧,为2的放在右侧,同样记下称量结果;
每一轮都按这个顺序进行,一共要称n次,最终结果是个n位的编码;
如果编码等于某个小球的正序码,则这个小球比其它球重;
如果编码等于某个小球的逆序码,则这个小球比其它球轻。
下面就是这个算法的完整演示:
首先输入球数,电脑会自动给所有球编码;然后手工设置某个特殊球是轻还是重;接下来就会自动分组称量,最终找到特殊球,看看是否和你所设置的那个一致。
在本演示中,绿色代表轻;红色代表重。
补充说明:
- 如果小球的数量是3的倍数,则上面的算法完全没有问题,但如果不是3的倍数,则要做如下处理:
小球数量除以3,余1,则给多出来的这个球分配以1开头的编号;
小球数量除以3,余2,则给多出来的这两个球分配一组编号中以0和2开头的两个。
这样的话,第一轮称重的天平左右两侧球数必然相同。
而且每一轮称重后,都会有1/3或2/3的球被证明是重量正常的。所以如果后面出现天平左右球数不等,就找一个正常球补到少的一边,或者从多的一边取走一个正常球即可。 - 此算法适用于大于3的任何球数,限于浏览器性能,最多可输入999个;
- 本演示程序参考了知乎问题有999个乒乓球其中有一个和其他的质量不同,问你用天平最少几次一定能称出来?答案中洪涛提供的文章和陳浩的算法解释,在此特别致谢。
你式子打错了吧 /xk /xk 😅😅😅😅😅😅😅😅😅😅😅😅😅😅😅😅😅😅😅😅
博主你好,https://freemind.pluskid.org/machine-learning/a-compressed-sense-of-compressive-sensing-ii/ 这里提到的用矩阵方法来解决。通过矩阵的方法,似乎更为直观地找出有问题的硬币。我归纳了一下,这个求矩阵的问题:输入x(x是大于等于3的整数),得到一个n行x列的矩阵,n=⌈(2x+3)^1/3⌉ (向上取整,比如x=12,n=3;x=38,n=4;x=66,n=5)。这个矩阵满足:
1、不能出现全零的列;
2、任意两列不同;
3、任意两列的和不为零向量;
4、元素只能是-1,1或0;
5、每一行元素的和为0。
我是编程小白,请问博主,你能实现这个么?
这个方法很通用,但我想了想,实际操作性可能不是太强,如果现实中有 很多个球,如果不依赖计算机,光三进制编号就能把人弄晕了。
感觉这类问题更适合用动态规划,这样每次称球的数量可以减少,到最后一步就 1 vs 1 ,这样也更加符合普通人的思维方式。
利用原论文的证明,我在这篇文章的最后给出了动态规划的方法,可能更加直观一点:https://zhuanlan.zhihu.com/p/368050985
编号方法很不错。但我觉得现实中最常见的12个球问题,可以直接把顺序给背下来唬人用……如果真的太多还是上计算机为好
公式错了,n次最多可以从(3^n-1)/2个球中找出质量不同的小球,n>2。
譬如13个小球,3次就可以找出质量不同的那个球。
作者你的表述要严格一点呀,大标题是找到有问题的球,但正文里面却是找到有问题的球并判断轻重。这两个是有实际影响的,比如不考虑特殊球的轻重,两次称重最大可以在四个球中找到特殊的那个;要是考虑轻重,则两次称重最大只能在三个球中找到特殊的那个(就是那个公式)。
那个文献不太好找,因此也就只能默认了。
不过问题是,如果不考虑那个特殊球具体是轻是重,称n次最大可以从多少个球中找到特殊的那个呢?(看网上的视频,据说在不考虑轻重的情况下,可以在13个球中称三次找到特殊那个)
确实如此,省略的有些不对,我改一下。
12个球是三次,我们信息论需要做的作业。另外。。。求源码。。。。
3次这个问题是chromium浏览器内核的bug,明明是整除结果出了小数位。我加一层过滤之后就解决了。
源码已经有了,这么多年居然一直都是混淆过的版本,没注意。
请问 这样编码以后根据什么判断轻重的
嘿大神 根据知乎上给出的结论 n次称量最多(3^n-3)/2个硬币,12枚硬币应该是3次,而你的演示是4次?
源码混淆过了啊
站长求代码!
站长,求代码呀
公式有问题,39个必须称5次。
没问题啊,39个也可以4次解决,拿程序演示一下就可以
有bug,12个球程序说需要4轮,但是只需要3轮就可以
继续点赞。。
鼓掌
我是金苹果锦城一中的学生
现在有11个球,编号从1到11,其中最多有一个不知道更重还是更轻的次品,请问你最少需要用天平称多少次才能找到这个次品球,并确定它是更重还是更轻?请写出你的方案的前两次称量的步骤。
你知道这道题的答案吗
ps.我是傻逼